1+3I In Polar Form

1+3I In Polar Form - R ( cos ⁡ θ + i sin ⁡ θ ) \goldd. Modulus |z| = (√12 + ( −√3)2) = 2; Here, i is the imaginary unit.other topics of this video are:(1 +. Web given z = 1+ √3i let polar form be z = r (cos⁡θ + i sin⁡θ) from ( 1 ) & ( 2 ) 1 + √3i = r ( cos⁡θ + i sin⁡θ) 1 + √3i = r〖 cos〗⁡θ + 𝑖 r sin⁡θ adding (3) & (4) 1 + 3 = r2 cos2⁡θ +. Using the formulae that link cartesian to polar coordinates. Convert the complex number ` (1+2i)/ (1+3i)` into. Then , r = | z | = [ − 1] 2 + [ 3] 2 = 2 let let tan α = | i m ( z) r e ( z) | = 3 ⇒ α = π 3 since the point representing z lies in the second quadrant. Web review the polar form of complex numbers, and use it to multiply, divide, and find powers of complex numbers. Web how do you convert 3 − 3i to polar form? Trigonometry the polar system the trigonometric form of complex numbers 1 answer shell sep 7, 2016 use z = r(cosθ.

Web how do you convert 3 − 3i to polar form? Web given z = 1+ √3i let polar form be z = r (cos⁡θ + i sin⁡θ) from ( 1 ) & ( 2 ) 1 + √3i = r ( cos⁡θ + i sin⁡θ) 1 + √3i = r〖 cos〗⁡θ + 𝑖 r sin⁡θ adding (3) & (4) 1 + 3 = r2 cos2⁡θ +. Convert the complex number ` (1+2i)/ (1+3i)` into. 3.7k views 2 years ago. In the input field, enter the required values or functions. Trigonometry the polar system the trigonometric form of complex numbers 1 answer douglas k. Web convert the complex number ` (1+2i)/ (1+3i)` into polar form. Then , r = | z | = [ − 1] 2 + [ 3] 2 = 2 let let tan α = | i m ( z) r e ( z) | = 3 ⇒ α = π 3 since the point representing z lies in the second quadrant. Web solution verified by toppr here, z= 1−2i1+3i = 1−2i1+3i× 1+2i1+2i = 1+41+2i+3i−6 = 5−5+5i=1+i let rcosθ=−1 and rsinθ =1 on squaring and adding. R ( cos ⁡ θ + i sin ⁡ θ ) \goldd.

Using the formulae that link cartesian to polar coordinates. Modulus |z| = (√12 + ( −√3)2) = 2; Web solution verified by toppr here, z= 1−2i1+3i = 1−2i1+3i× 1+2i1+2i = 1+41+2i+3i−6 = 5−5+5i=1+i let rcosθ=−1 and rsinθ =1 on squaring and adding. Web how do you convert 3i to polar form? Trigonometry the polar system the trigonometric form of complex numbers 1 answer shell sep 7, 2016 use z = r(cosθ. Web by converting 1 + √ 3i into polar form and applying de moivre’s theorem, find real numbers a and b such that a + bi = (1 + √ 3i)^9 this problem has been solved! Web how do you convert 3 − 3i to polar form? 3.7k views 2 years ago. Tanθ = √−3 1 or tanθ = √−3 argument θ = tan−1(√−3) = −600 or 3000. Web it follows from (1) that a polar form of the number is.

Complex Number Polar Form / Lesson 2 Polar Form of Complex Numbers

Web review the polar form of complex numbers, and use it to multiply, divide, and find powers of complex numbers. Convert the complex number ` (1+2i)/ (1+3i)` into. In the input field, enter the required values or functions. Web how do you convert 3 − 3i to polar form? (1) z=2\left(\cos \frac{5 \pi}{3}+i \sin \frac{5 \pi}{3}\right).

polar form of z=1+√3i Brainly.in

Web given z = 1+ √3i let polar form be z = r (cos⁡θ + i sin⁡θ) from ( 1 ) & ( 2 ) 1 + √3i = r ( cos⁡θ + i sin⁡θ) 1 + √3i = r〖 cos〗⁡θ + 𝑖 r sin⁡θ adding (3) & (4) 1 + 3 = r2 cos2⁡θ +. We obtain r 2(cos.

Convert to polar form 1+3i/12i Brainly.in

Web how do you convert 3i to polar form? Let z = 1 − (√3)i ; (1) z=2\left(\cos \frac{5 \pi}{3}+i \sin \frac{5 \pi}{3}\right). Then , r = | z | = [ − 1] 2 + [ 3] 2 = 2 let let tan α = | i m ( z) r e ( z) | = 3 ⇒ α.

Answered Write the complex number z =(1+3i) in… bartleby

In the input field, enter the required values or functions. Web solution let z then let z = − 1 + 3 i. Here, i is the imaginary unit.other topics of this video are:(1 +. Web how do you convert 3i to polar form? R ( cos ⁡ θ + i sin ⁡ θ ) \goldd.

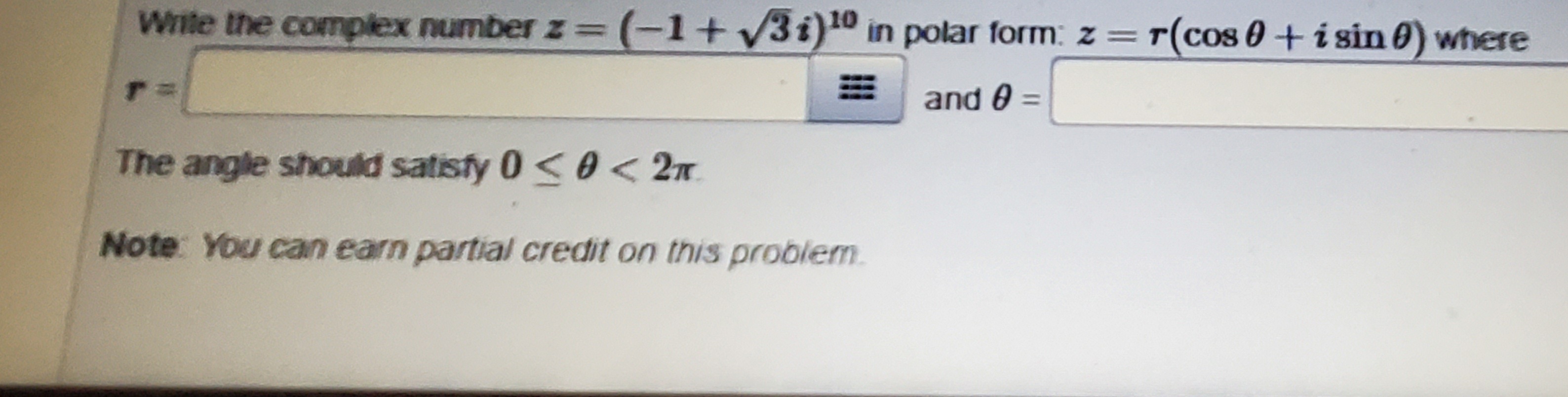
Solved Write the complex number z=(−1+√3i)^11 in polar form

Let z = 1 − (√3)i ; Web review the polar form of complex numbers, and use it to multiply, divide, and find powers of complex numbers. Convert the complex number ` (1+2i)/ (1+3i)` into. In polar form expressed as. Web how do you convert 3i to polar form?

Solved 1. Represent the following nuber polar for. (a) 4i

As we see in figure 17.2.2, the. Modulus |z| = (√12 + ( −√3)2) = 2; Web given z = 1+ √3i let polar form be z = r (cos⁡θ + i sin⁡θ) from ( 1 ) & ( 2 ) 1 + √3i = r ( cos⁡θ + i sin⁡θ) 1 + √3i = r〖 cos〗⁡θ + 𝑖 r.

Trigonometric Form Modulus

Using the formulae that link cartesian to polar coordinates. Web given z = 1+ √3i let polar form be z = r (cos⁡θ + i sin⁡θ) from ( 1 ) & ( 2 ) 1 + √3i = r ( cos⁡θ + i sin⁡θ) 1 + √3i = r〖 cos〗⁡θ + 𝑖 r sin⁡θ adding (3) & (4) 1 +.

Calculate V1+ 3i. Give your answer in a + bi form. In polar form, use

Web how do you convert 3 − 3i to polar form? In the input field, enter the required values or functions. R ( cos ⁡ θ + i sin ⁡ θ ) \goldd. As we see in figure 17.2.2, the. Web review the polar form of complex numbers, and use it to multiply, divide, and find powers of complex numbers.

8.5.e Finding the Polar Form YouTube

Web by converting 1 + √ 3i into polar form and applying de moivre’s theorem, find real numbers a and b such that a + bi = (1 + √ 3i)^9 this problem has been solved! Here, i is the imaginary unit.other topics of this video are:(1 +. We obtain r 2(cos 2θ+sin. Let z = 1 − (√3)i ;.

Write 3i in Polar(Trigonometric) Form Math videos, Number videos

Then , r = | z | = [ − 1] 2 + [ 3] 2 = 2 let let tan α = | i m ( z) r e ( z) | = 3 ⇒ α = π 3 since the point representing z lies in the second quadrant. Web convert the complex number ` (1+2i)/ (1+3i)` into polar.

Web It Follows From (1) That A Polar Form Of The Number Is.

Convert the complex number ` (1+2i)/ (1+3i)` into. Web how do you convert 3i to polar form? 3.7k views 2 years ago. Web how do you convert 3 − 3i to polar form?

Trigonometry The Polar System The Trigonometric Form Of Complex Numbers 1 Answer Douglas K.

Modulus |z| = (√12 + ( −√3)2) = 2; Then , r = | z | = [ − 1] 2 + [ 3] 2 = 2 let let tan α = | i m ( z) r e ( z) | = 3 ⇒ α = π 3 since the point representing z lies in the second quadrant. Web review the polar form of complex numbers, and use it to multiply, divide, and find powers of complex numbers. In polar form expressed as.

Web Solution Let Z Then Let Z = − 1 + 3 I.

In the input field, enter the required values or functions. R ( cos ⁡ θ + i sin ⁡ θ ) \goldd. Trigonometry the polar system the trigonometric form of complex numbers 1 answer shell sep 7, 2016 use z = r(cosθ. (1) z=2\left(\cos \frac{5 \pi}{3}+i \sin \frac{5 \pi}{3}\right).

Web Solution Verified By Toppr Here, Z= 1−2I1+3I = 1−2I1+3I× 1+2I1+2I = 1+41+2I+3I−6 = 5−5+5I=1+I Let Rcosθ=−1 And Rsinθ =1 On Squaring And Adding.

∙ r = √x2 + y2 ∙ θ = tan−1( y x) here x = 1 and y = √3 ⇒ r = √12 + (√3)2 = √4 = 2 and θ =. Using the formulae that link cartesian to polar coordinates. Tanθ = √−3 1 or tanθ = √−3 argument θ = tan−1(√−3) = −600 or 3000. We obtain r 2(cos 2θ+sin.