Cartesian Form Vector
Cartesian Form Vector - Finding three points on the plane by setting two variables equal to 0: Where λ ∈ r, and is a scalar/parameter In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in euclidean space. Web solution conversion of cartesian to vector : This can be done using two simple techniques. By working with just the geometric definition of the magnitude and direction of vectors, we were able to define operations such as addition, subtraction, and multiplication by scalars. Write the direction vector, b = a + b + c write the vector form of the equation as r = a + λ b. Web the cartesian form of a plane can be represented as ax + by + cz = d where a, b, and c are direction cosines that are normal to the plane and d is the distance from the origin to the plane. How do i find the a, b, c, s, e, f, g, t, h, i, j a, b, c, s, e, f, g,. Web cartesian coordinates in the introduction to vectors, we discussed vectors without reference to any coordinate system.
Cartesian coordinates, polar coordinates, parametric equations. First, the arbitrary form of vector [math processing error] r → is written as [math processing error] r → = x i ^ + y j ^ + z k ^. Magnitude & direction form of vectors. In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in euclidean space. The vector form can be easily converted into cartesian form by 2 simple methods. The plane containing a, b, c. Web write given the cartesian equation in standard form. Find u→ in cartesian form if u→ is a vector in the first quadrant, ∣u→∣=8 and the direction of u→ is 75° in standard position. The following video goes through each example to show you how you can express each force in cartesian vector form. Show that the vectors and have the same magnitude.
Web there are usually three ways a force is shown. (a, b, c) + s (e, f, g) + t (h, i, j) so basically, my question is: For example, 7 x + y + 4 z = 31 that passes through the point ( 1, 4, 5) is ( 1, 4, 5) + s ( 4, 0, − 7) + t ( 0, 4, − 1) , s, t in r. By working with just the geometric definition of the magnitude and direction of vectors, we were able to define operations such as addition, subtraction, and multiplication by scalars. Terms and formulas from algebra i to calculus. Get full lessons & more subjects at: The plane containing a, b, c. Web solution conversion of cartesian to vector : Find u→ in cartesian form if u→ is a vector in the first quadrant, ∣u→∣=8 and the direction of u→ is 75° in standard position. Web this is just a few minutes of a complete course.
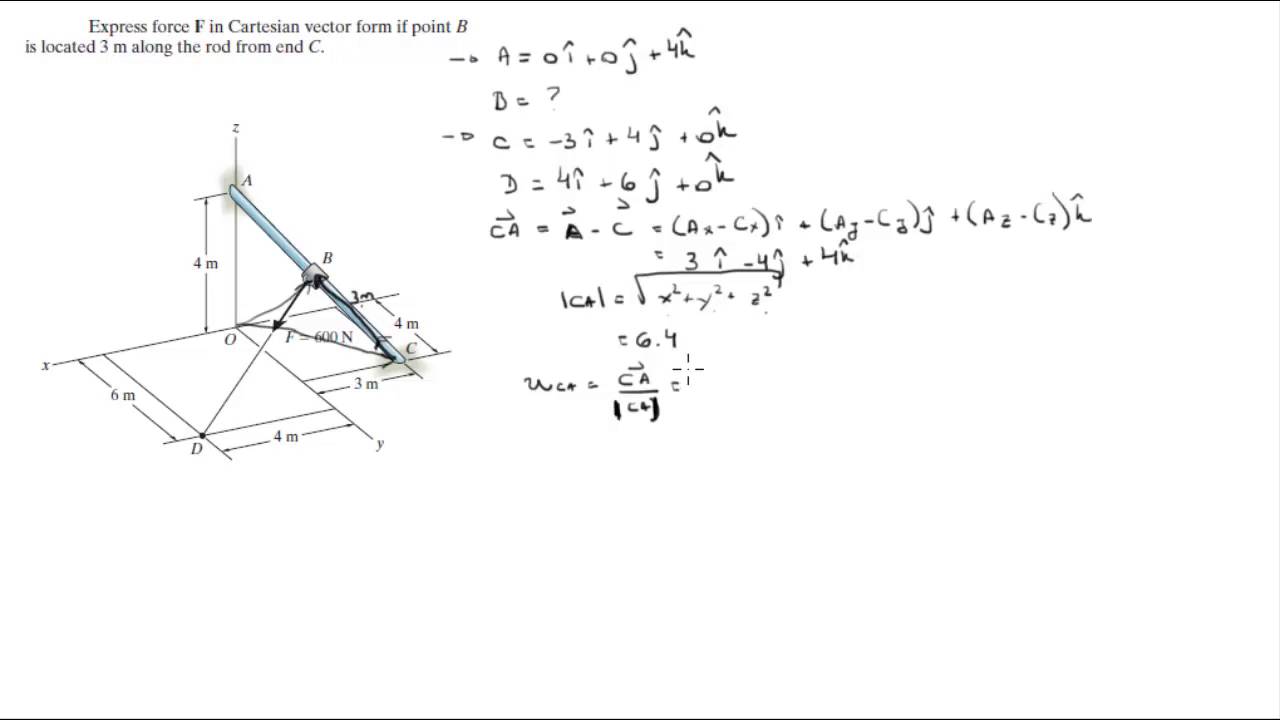
Express F in Cartesian Vector form YouTube
In cartesian form, a vector a is represented as a = a x i + a y j + a z k. First find two vectors in the plane: (a, b, c) + s (e, f, g) + t (h, i, j) so basically, my question is: Web there are usually three ways a force is shown. The plane containing.
PPT FORCE VECTORS, VECTOR OPERATIONS & ADDITION OF FORCES 2D & 3D
Round each of the coordinates to one decimal place. Web cartesian form of vector. Web explain the meaning of the unit vectors i,jandk express two dimensional and three dimensional vectors in cartesian form find the modulus of a vector expressed incartesian form find a ‘position vector’ 17 % your solution −→ oa= −−→ ob= answer −→ oa=a= 3i+ 5j, −−→.
Example 17 Find vector cartesian equations of plane passing Exampl
First find two vectors in the plane: The vector equation of a line is \vec {r} = 3\hat {i} + 2\hat {j} + \hat {k} + \lambda ( \hat {i} + 9\hat {j} + 7\hat {k}) r = 3i^+ 2j ^+ k^ + λ(i^+9j ^ + 7k^), where \lambda λ is a parameter. (i) using the arbitrary form of vector.
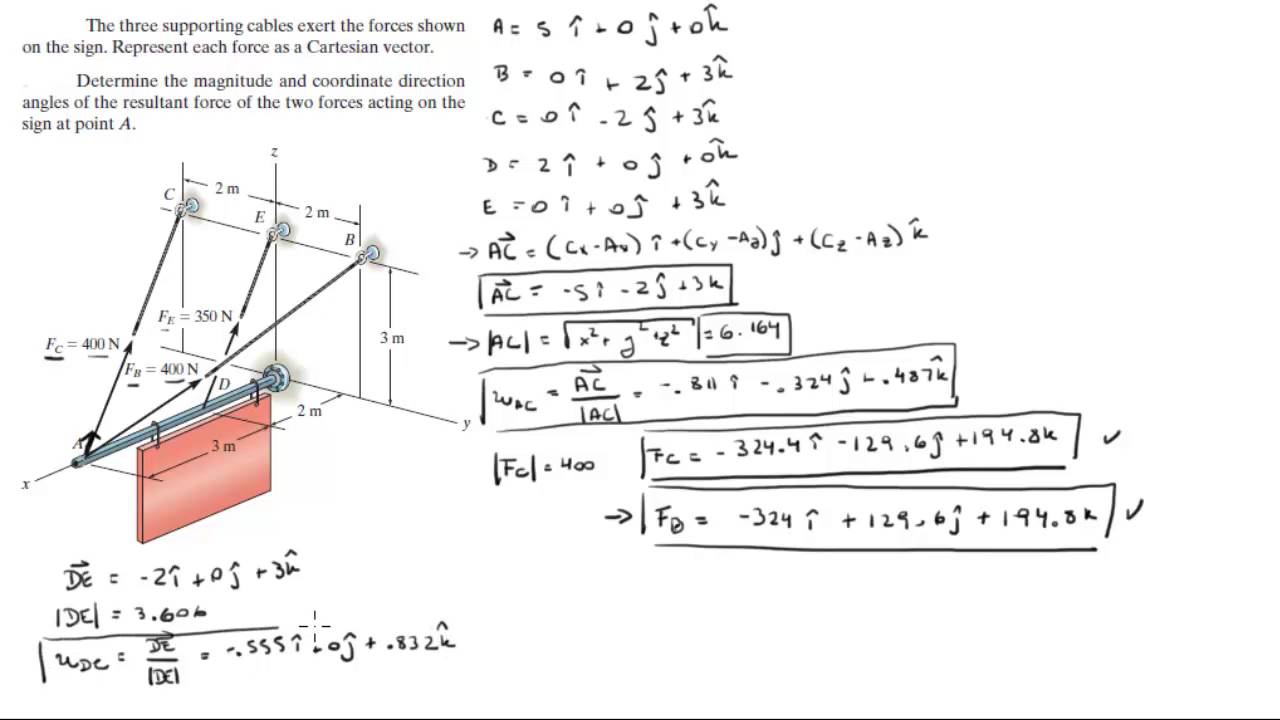
Find the Cartesian Vector form of the three forces on the sign and the
Web this is just a few minutes of a complete course. Find u→ in cartesian form if u→ is a vector in the first quadrant, ∣u→∣=8 and the direction of u→ is 75° in standard position. Finding three points on the plane by setting two variables equal to 0: Terms and formulas from algebra i to calculus. The vector equation.
Bab2
A vector decomposed (resolved) into its rectangular components can be expressed by using two possible notations namely the scalar notation (scalar components) and the cartesian vector notation. First, the arbitrary form of vector [math processing error] r → is written as [math processing error] r → = x i ^ + y j ^ + z k ^. Solution both.
Ex 11.2, 5 Find equation of line in vector, cartesian form
First, the arbitrary form of vector [math processing error] r → is written as [math processing error] r → = x i ^ + y j ^ + z k ^. Web cartesian coordinates in the introduction to vectors, we discussed vectors without reference to any coordinate system. A = x 1 + y 1 + z 1; Terms and.
Express each in Cartesian Vector form and find the resultant force
Web the cartesian form of a plane can be represented as ax + by + cz = d where a, b, and c are direction cosines that are normal to the plane and d is the distance from the origin to the plane. Find u→ in cartesian form if u→ is a vector in the first quadrant, ∣u→∣=8 and the.
Example 8 The Cartesian equation of a line is. Find vector
In this unit we describe these unit vectors in two dimensions and in threedimensions, and show how they can be used in calculations. A vector decomposed (resolved) into its rectangular components can be expressed by using two possible notations namely the scalar notation (scalar components) and the cartesian vector notation. Write the direction vector, b = a + b +.
Resultant Vector In Cartesian Form RESTULS
Find u→ in cartesian form if u→ is a vector in the first quadrant, ∣u→∣=8 and the direction of u→ is 75° in standard position. In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in euclidean space. The direction ratios of the line are a, b, and c. Web to find the.
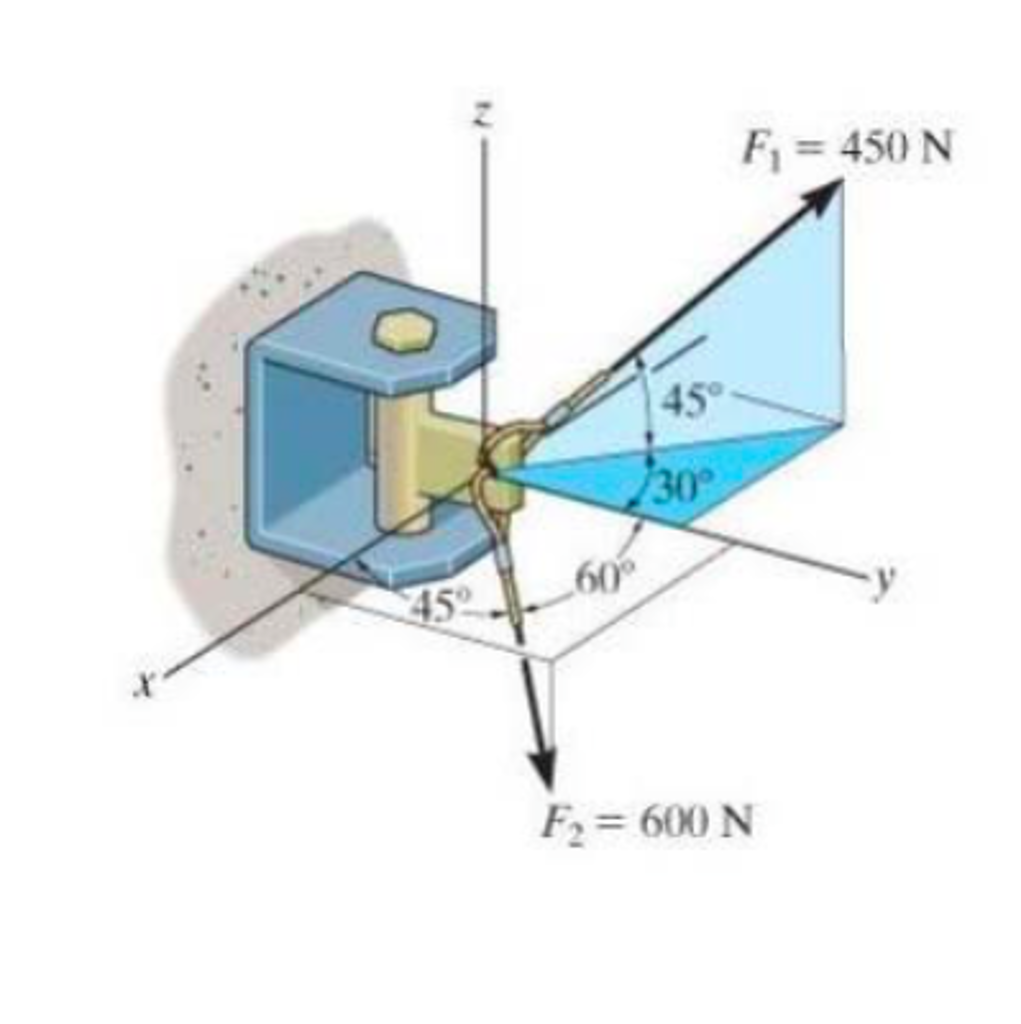
Solved 1. Write both the force vectors in Cartesian form.
The vector form can be easily converted into cartesian form by 2 simple methods. (a, b, c) + s (e, f, g) + t (h, i, j) so basically, my question is: Web viewed 16k times. First find two vectors in the plane: In this way, following the parallelogram rule for vector addition, each vector on a cartesian plane can.
For Example, 7 X + Y + 4 Z = 31 That Passes Through The Point ( 1, 4, 5) Is ( 1, 4, 5) + S ( 4, 0, − 7) + T ( 0, 4, − 1) , S, T In R.
The following video goes through each example to show you how you can express each force in cartesian vector form. Web solution conversion of cartesian to vector : Web there are usually three ways a force is shown. Web viewed 16k times.
In This Way, Following The Parallelogram Rule For Vector Addition, Each Vector On A Cartesian Plane Can Be Expressed As The Vector Sum Of Its Vector Components:
(a, b, c) + s (e, f, g) + t (h, i, j) so basically, my question is: A = x 1 + y 1 + z 1; Here is what i have tried: By working with just the geometric definition of the magnitude and direction of vectors, we were able to define operations such as addition, subtraction, and multiplication by scalars.
Web This Is Just A Few Minutes Of A Complete Course.
Show that the vectors and have the same magnitude. The components of a vector along orthogonal axes are called rectangular components or cartesian components. The vector equation of a line is \vec {r} = 3\hat {i} + 2\hat {j} + \hat {k} + \lambda ( \hat {i} + 9\hat {j} + 7\hat {k}) r = 3i^+ 2j ^+ k^ + λ(i^+9j ^ + 7k^), where \lambda λ is a parameter. First, the arbitrary form of vector [math processing error] r → is written as [math processing error] r → = x i ^ + y j ^ + z k ^.
Write The Direction Vector, B = A + B + C Write The Vector Form Of The Equation As R = A + Λ B.
Cartesian coordinates, polar coordinates, parametric equations. Solution both vectors are in cartesian form and their lengths can be calculated using the formula we have and therefore two given vectors have the same length. In this unit we describe these unit vectors in two dimensions and in threedimensions, and show how they can be used in calculations. In cartesian form, a vector a is represented as a = a x i + a y j + a z k.