Row Echelon Form Vs Reduced Row Echelon Form
Row Echelon Form Vs Reduced Row Echelon Form - Web reduced row echelon form we have seen that every linear system of equations can be written in matrix form. Web learn to replace a system of linear equations by an augmented matrix. Web echelon form of a matrix. How do these differ from the reduced row echelon matrix of the associated augmented matrix? 5.each leading 1 is the only nonzero entry in its column. 4.the leading entry in each nonzero row is 1. Web many of the problems you will solve in linear algebra require that a matrix be converted into one of two forms, the row echelon form (ref) and its stricter variant. This lesson introduces the concept of an echelon matrix. All nonzero rows are above all rows of zeros. Web theorem 1 (uniqueness of the reduced echelon form).
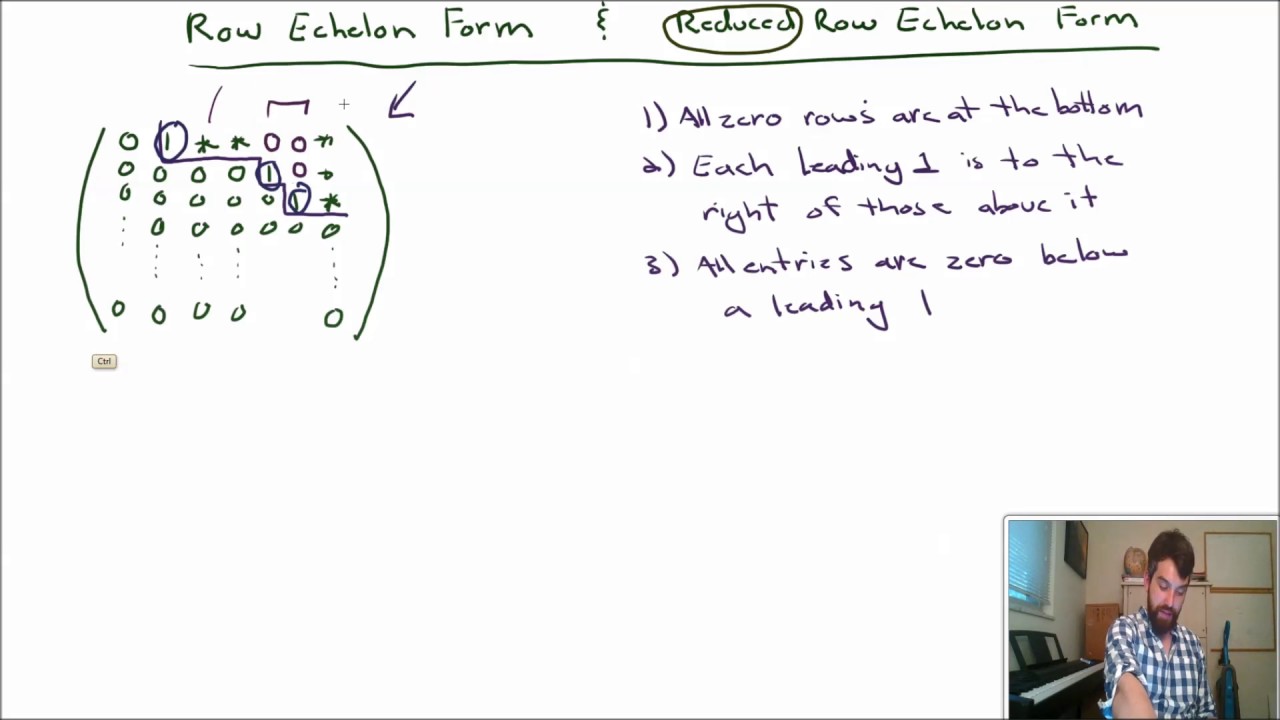
All entries in a column below a leading entry are zeros. Echelon matrices come in two forms: Web a reduced echelon form matrix has the additional properties that (1) every leading entry is a 1 and (2) in any column that contains a leading entry, that leading entry is the only non. For it to be in. For the proof, we need to wait until we learn. Web reduced echelon form or reduced row echelon form: This lesson introduces the concept of an echelon matrix. The row echelon form (ref) and the reduced row. The leading entry of any row is to the. This means that the matrix meets the following three requirements:
The row echelon form (ref) and the reduced row. Web echelon form of a matrix. This lesson introduces the concept of an echelon matrix. This means that the matrix meets the following three requirements: Web learn to replace a system of linear equations by an augmented matrix. Web definition (row echelon form) a matrix m is said to be in row echelon form (ref) iff: Each matrix is row equivalent to one and only one reduced echelon matrix. Web compute the reduced row echelon form of each coefficient matrix. The first number in the row (called a leading. Web reduced row echelon form we have seen that every linear system of equations can be written in matrix form.
Transforming Square Matrices Into Reduced Row Echelon Form 7 Steps
Web instead of gaussian elimination and back substitution, a system of equations can be solved by bringing a matrix to reduced row echelon form. The first number in the row (called a leading. Echelon matrices come in two forms: All nonzero rows are above all rows of zeros. All entries in a column below a leading entry are zeros.
PPT ROWECHELON FORM AND REDUCED ROWECHELON FORM PowerPoint
For it to be in. Each matrix is row equivalent to one and only one reduced echelon matrix. All nonzero rows are above all rows of zeros. 5.each leading 1 is the only nonzero entry in its column. This lesson introduces the concept of an echelon matrix.
Reduced Echelon Form & Row Reduction Algorithm YouTube
All nonzero rows are above all rows of zeros. Web reduced echelon form or reduced row echelon form: The first number in the row (called a leading. Each matrix is row equivalent to one and only one reduced echelon matrix. Learn how the elimination method corresponds to performing row operations on an augmented.
Row Echelon Form of a Matrix YouTube
This means that the matrix meets the following three requirements: Web echelon form of a matrix. Web a reduced echelon form matrix has the additional properties that (1) every leading entry is a 1 and (2) in any column that contains a leading entry, that leading entry is the only non. Web reduced echelon form or reduced row echelon form:.
Echlon Form How To Reduce A Matrix To Row Echelon Form 8 Steps
This means that the matrix meets the following three requirements: Each leading entry of a row is in a column to the right of the leading entry of the row above it. Web reduced echelon form or reduced row echelon form: For it to be in. For the proof, we need to wait until we learn.
Row Echelon Form and Reduced Row Echelon Form YouTube
Web theorem 1 (uniqueness of the reduced echelon form). Learn how the elimination method corresponds to performing row operations on an augmented. Web reduced row echelon form we have seen that every linear system of equations can be written in matrix form. 4.the leading entry in each nonzero row is 1. Web definition (row echelon form) a matrix m is.
PPT Elementary Linear Algebra PowerPoint Presentation, free download
Web learn to replace a system of linear equations by an augmented matrix. Web echelon form of a matrix. 4.the leading entry in each nonzero row is 1. The row echelon form (ref) and the reduced row. How do these differ from the reduced row echelon matrix of the associated augmented matrix?
Tutorial 0 mth 3201
Web learn to replace a system of linear equations by an augmented matrix. This means that the matrix meets the following three requirements: Web a reduced echelon form matrix has the additional properties that (1) every leading entry is a 1 and (2) in any column that contains a leading entry, that leading entry is the only non. Each matrix.
Row Echelon (REF) vs. Reduced Row Echelon Form (RREF) TI 84 Calculator
Web definition (row echelon form) a matrix m is said to be in row echelon form (ref) iff: Web a reduced echelon form matrix has the additional properties that (1) every leading entry is a 1 and (2) in any column that contains a leading entry, that leading entry is the only non. This lesson introduces the concept of an.
Uniqueness of Reduced Row Echelon Form YouTube
All nonzero rows are above all rows of zeros. Each leading entry of a row is in a column to the right of the leading entry of the row above it. Web reduced echelon form or reduced row echelon form: For the proof, we need to wait until we learn. Web learn to replace a system of linear equations by.
The Row Echelon Form (Ref) And The Reduced Row.
Each leading entry of a row is in a column to the right of the leading entry of the row above it. For the proof, we need to wait until we learn. Web theorem 1 (uniqueness of the reduced echelon form). Web instead of gaussian elimination and back substitution, a system of equations can be solved by bringing a matrix to reduced row echelon form.
The First Number In The Row (Called A Leading.
This means that the matrix meets the following three requirements: 5.each leading 1 is the only nonzero entry in its column. The leading entry of any row is to the. Web definition (row echelon form) a matrix m is said to be in row echelon form (ref) iff:
Web Echelon Form Of A Matrix.
Web a reduced echelon form matrix has the additional properties that (1) every leading entry is a 1 and (2) in any column that contains a leading entry, that leading entry is the only non. Web compute the reduced row echelon form of each coefficient matrix. All entries in a column below a leading entry are zeros. Web reduced row echelon form we have seen that every linear system of equations can be written in matrix form.
For Example, The System X+ 2Y + 3Z = 4 3X+ 4Y + Z = 5 2X+.
Web reduced echelon form or reduced row echelon form: Web many of the problems you will solve in linear algebra require that a matrix be converted into one of two forms, the row echelon form (ref) and its stricter variant. Each matrix is row equivalent to one and only one reduced echelon matrix. Learn how the elimination method corresponds to performing row operations on an augmented.