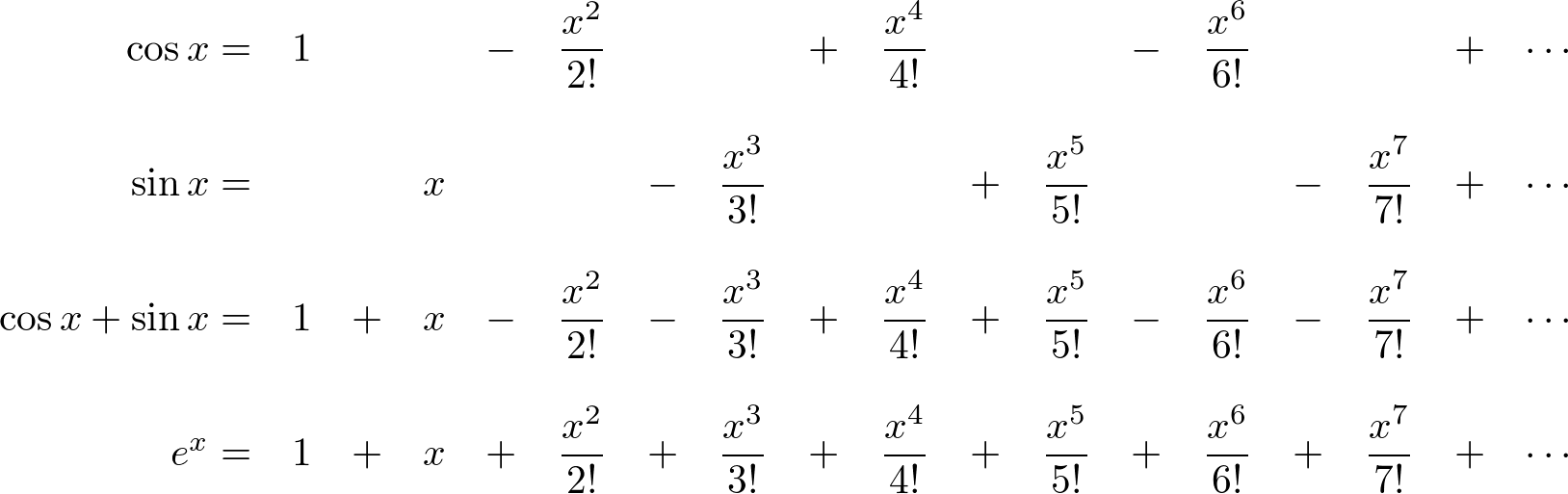Sinx In Exponential Form
Sinx In Exponential Form - Sinz denotes the complex sine function. Sinz = exp(iz) − exp( − iz) 2i. Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. E^(ix) = sum_(n=0)^oo (ix)^n/(n!) = sum_(n. Expz denotes the exponential function. But i could also write the sine function as the imaginary part of the exponential. The picture of the unit circle and these coordinates looks like this: Web notes on the complex exponential and sine functions (x1.5) i. Web relations between cosine, sine and exponential functions. E^x = sum_(n=0)^oo x^n/(n!) so:
E^x = sum_(n=0)^oo x^n/(n!) so: Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. Sinz denotes the complex sine function. Web in mathematics, physics and engineering, the sinc function, denoted by sinc (x), has two forms, normalized and unnormalized. Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Sin ( i x) = 1 2 i ( exp ( − x) − exp ( x)) = i sinh ( x). Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix e i x in exponential form, of course you could write eix = cos(x). Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. For any complex number z : If μ r then eiμ def = cos μ + i sin μ.
Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix e i x in exponential form, of course you could write eix = cos(x). But i could also write the sine function as the imaginary part of the exponential. Periodicity of the imaginary exponential. [1] 0:03 the sinc function as audio, at 2000 hz. Web in mathematics, physics and engineering, the sinc function, denoted by sinc (x), has two forms, normalized and unnormalized. Web may 31, 2014 at 18:57. Web i know that in general i can use. Web notes on the complex exponential and sine functions (x1.5) i. This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers.
Solving Exponential Trigonometric Equations 81^sin2x+81^cos^2x=30
This formula can be interpreted as saying that the function e is a unit complex number, i.e., it traces out the unit circle in the complex plane as φ ranges through the real numbers. Web in mathematics, physics and engineering, the sinc function, denoted by sinc (x), has two forms, normalized and unnormalized. For any complex number z : Sin(x).
How to Integrate Exponential and Trigonometric Functions (e^x)(Sinx
Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. For any complex number z : But i could also write the sine function as the imaginary part of the exponential. Periodicity of the imaginary exponential. Web relations between cosine, sine and exponential functions.
Integral Table Pdf / List Of Integrals Of Exponential Functions Wikipedia
Sinz denotes the complex sine function. Sin ( i x) = 1 2 i ( exp ( − x) − exp ( x)) = i sinh ( x). Expz denotes the exponential function. The picture of the unit circle and these coordinates looks like this: Web may 31, 2014 at 18:57.
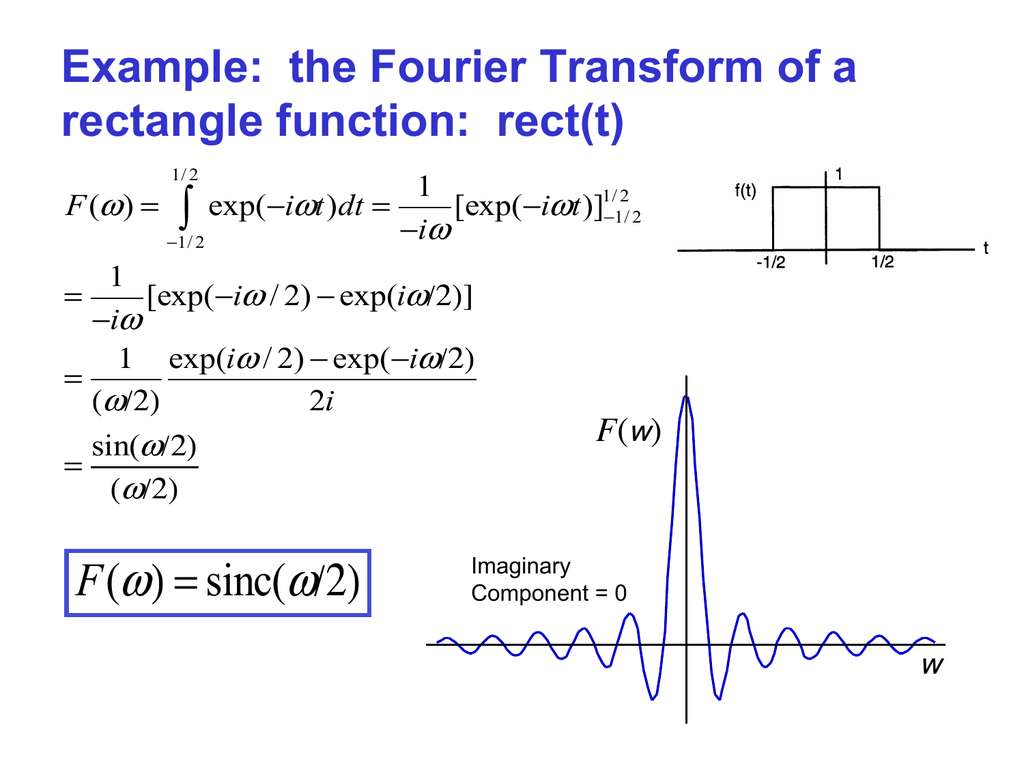
( sinc( F ω ) = /2)
Web relations between cosine, sine and exponential functions. Sinz = exp(iz) − exp( − iz) 2i. Web specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions, [10] and are used to obtain an angle from any of the angle's. But i could also write the sine function as the imaginary part of the exponential..
How to Solve cos(x) + sin(2x) = 0 (Trigonometric Equations) YouTube
But i could also write the sine function as the imaginary part of the exponential. For any complex number z : Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Sin ( i x) = 1 2 i ( exp ( − x) − exp.
graphs of sinx and cosx in hindi maths YouTube
Expz denotes the exponential function. Web may 31, 2014 at 18:57. E^x = sum_(n=0)^oo x^n/(n!) so: Web in mathematics, physics and engineering, the sinc function, denoted by sinc (x), has two forms, normalized and unnormalized. Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix.
Grade 12 Advanced Functions [licensed for use only
Sinz = exp(iz) − exp( − iz) 2i. E^x = sum_(n=0)^oo x^n/(n!) so: Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Expz denotes the exponential function. Here φ is the angle that a line connecting the origin with a point on the unit circle.
Function For Sine Wave Between Two Exponential Cuves Mathematics
Web relations between cosine, sine and exponential functions. Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix e i x in exponential form, of course you could write eix = cos(x). [1] 0:03 the sinc function as audio, at 2000 hz. Web trigonometric substitution.
Proof that the derivative of coshx is sinhx Maths exam, Math videos
Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix e i x in exponential form, of course you could write eix = cos(x). (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Expz denotes the exponential.
Solved 5. Euler's equations are defined as sin (x) cos(x) e"
For any complex number z : Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians. Sinz = exp(iz) − exp( − iz) 2i. E^x = sum_(n=0)^oo x^n/(n!) so: Web trigonometric substitution integrals ( inverse functions) derivatives v t e in.
Web I Know That In General I Can Use.
Web euler’s formula for complex exponentials according to euler, we should regard the complex exponential eit as related to the trigonometric functions cos(t) and. Web notes on the complex exponential and sine functions (x1.5) i. Web relations between cosine, sine and exponential functions. For any complex number z :
This Formula Can Be Interpreted As Saying That The Function E Is A Unit Complex Number, I.e., It Traces Out The Unit Circle In The Complex Plane As Φ Ranges Through The Real Numbers.
Sinz denotes the complex sine function. Sin ( i x) = 1 2 i ( exp ( − x) − exp ( x)) = i sinh ( x). (45) (46) (47) from these relations and the properties of exponential multiplication you can painlessly prove all. Sin(x) sin ( x) is the fourier series of sin(x) sin ( x) just as eix e i x is the fourier series of eix e i x in exponential form, of course you could write eix = cos(x).
Web Specifically, They Are The Inverses Of The Sine, Cosine, Tangent, Cotangent, Secant, And Cosecant Functions, [10] And Are Used To Obtain An Angle From Any Of The Angle's.
But i could also write the sine function as the imaginary part of the exponential. Web may 31, 2014 at 18:57. The picture of the unit circle and these coordinates looks like this: Periodicity of the imaginary exponential.
[1] 0:03 The Sinc Function As Audio, At 2000 Hz.
Web in mathematics, physics and engineering, the sinc function, denoted by sinc (x), has two forms, normalized and unnormalized. If μ r then eiμ def = cos μ + i sin μ. E^x = sum_(n=0)^oo x^n/(n!) so: Here φ is the angle that a line connecting the origin with a point on the unit circle makes with the positive real axis, measured counterclockwise and in radians.